Research article
Inverse RNA folding solution based on multi-objective genetic algorithm and Gibbs sampling method
M Ganjtabesh1[*],2,3, F Zare-Mirakabad4, A Nowzari-Dalini1
1School of Mathematics, Statistics, and Computer Science, College of Science, University of Tehran, Tehran, Iran2School of Computer Science, Institute for Studies in Theoretical Physics and Mathematics (IPM), Tehran, Iran
3Laboratoire d’Informatique (LIX), Ecole Polytechnique, Palaiseau CEDEX, 91128, France
4Department of Applied Mathematics, Faculty of Mathematics and Computer Science, Amirkabir University of Technology, Tehran, Iran
EXCLI J 2013;12:Doc546
Abstract
In living systems, RNAs play important biological functions. The functional form of an RNA frequently requires a specific tertiary structure. The scaffold for this structure is provided by secondary structural elements that are hydrogen bonds within the molecule. Here, we concentrate on the inverse RNA folding problem. In this problem, an RNA secondary structure is given as a target structure and the goal is to design an RNA sequence that its structure is the same (or very similar) to the given target structure. Different heuristic search methods have been proposed for this problem. One common feature among these methods is to use a folding algorithm to evaluate the accuracy of the designed RNA sequence during the generation process. The well known folding algorithms take O(n3) times where n is the length of the RNA sequence. In this paper, we introduce a new algorithm called GGI-Fold based on multi-objective genetic algorithm and Gibbs sampling method for the inverse RNA folding problem. Our algorithm generates a sequence where its structure is the same or very similar to the given target structure. The key feature of our method is that it never uses any folding algorithm to improve the quality of the generated sequences. We compare our algorithm with RNA-SSD for some biological test samples. In all test samples, our algorithm outperforms the RNA-SSD method for generating a sequence where its structure is more stable.
Keywords: RNA structure, inverse RNA folding, genetic algorithm, Gibbs sampling
1. Introduction
RNAs perform a wide range of functions in biological systems. The functional form of RNA, frequently requires a specific tertiary structure. The scaffold for this structure is provided by secondary structural elements that are hydrogen bonds within the molecule. Therefore, the study and analysis of RNA secondary structures are critical to understand their functional roles inside the cell (Condon et al., 2004[7]; Higgs, 2000[13]; Hofacker et al., 1994[14]; Khan et al., 2011[16]; Shapiro, 1988[20]; Zare-Mirakabad et al., 2009[25]). In this sense, it is of great interest to propose computational techniques for predicting RNA secondary structural features. Most of the existing computational approaches are based on a thermodynamic model that minimizes the free energy value for each secondary structure (Zuker, 1994[26]). In other words, the stable structure of RNA has Minimum Free Energy (MFE).
One of the most important problem in RNA area is the inverse RNA folding. In this problem, a secondary structure of an RNA is given, and the goal is to find a proper sequence that folds into the given RNA secondary structure. The inverse RNA folding problem can be used to design the non-coding RNAs, which are involved in gene regulation, chromosome replication and RNA modification (Knight, 2003[17]; Cech, 2004[6]). Also the designed sequences are applicable to construct ribozymes and riboswitches, which may be used as drugs in therapeutic agents (Busch and Backofen, 2006[5]; Storz, 2002[22]), or for building self-assembling structures from small RNA molecules in nanobiotechnology (Aguirre-Hernández et al., 2007[1]). The inverse RNA folding can be considered as a multi-objective optimization problem. In this problem, there are exponentially many sequences to be considered as the candidates for the solution (Condon et al., 2004[7]; Haslinger and Stadler, 1999[12]; Ganjtabesh and Steyaert, 2011[8]). Also, the inverse RNA folding is not an easy problem. It is proved that for a given Hidden Markov Model (HMM) and target path, the existence of a sequence with the target path as Viterbi path (most probable path) is an NP-Complete problem (Schnall-Levin et al., 2008[19]). Therefore, it is not reasonable to find a global optimal solution by testing all candidate sequences and thus the heuristic search methods are used to address this problem (Hofacker et al., 1994[14]; Aguirre-Hernández et al., 2007[1]; Andronescu et al., 2004[3]; Busch and Backofen, 2006[5]; Ivry et al., 2009[15]; Gao et al., 2010[9]; Avihoo et al., 2011[4]; Taneda, 2011[23], 2012[24]).
RNAinverse, available as a part of the Vienna RNA package, is an original approach to solve this problem (Hofacker et al., 1994[14]). This algorithm uses a distance score to measure the distance between the structure of the designed sequence and the target structure. The goal of this algorithm is to minimize the distance score, as well as to maximize the probability of folding the designed sequence into the target structure. When this distance score becomes zero, the algorithm ends and the generated sequence is returned. The second algorithm called RNA-SSD (RNA Secondary Structure Designer) is developed by Andronescu et al. (2004[3]). RNA-SSD tries to minimize the structural distance via recursive stochastic local search. Busch and Backofen (2006[5]) proposed another algorithm based on dynamic programming and local search, called INFO-RNA. This algorithm consists of two steps. In the first step, it generates the initial sequences using dynamic programming. In the second step, it uses a stochastic local search method to improve the quality of the initial sequence. There is a recent algorithm for this problem based on image processing approach (Ivry et al., 2009[15]). This algorithm replaces the distance measure used by RNAinverse algorithm with a new image processing distance technique, and thus creates a new version of the algorithm for the inverse RNA folding problem. Genetic algorithm is also used to solve the inverse RNA folding problem, both for RNA secondary structure (Taneda, 2011[23]) and pseudoknotted structures (Taneda, 2012[24]).
It should be mentioned that the existing methods use a folding algorithm for evaluating and improving the accuracy and the quality of the generated sequences. Employing any folding algorithm requires at least O(n3) time steps. Therefore, it slows the overall running time of all proposed methods. On the other hand, any algorithm that uses a specified folding method will be biased to that method. In this paper, we present a new method to solve this problem without using any folding algorithm. Our new algorithm (GGI-Fold) is designed based on the multi-objective genetic algorithm and Gibbs sampling method. At first, GGI-Fold designs a sub-sequence for each sub-structure of the target structure based on genetic algorithm. Then all sub-sequences are updated by Gibbs sampling method. Finally, the sub-sequences are assembled to construct a sequence corresponding to the target structure. In this approach, our main effort is to generate feasible sub-sequences corresponding to sub-structures in such a way that the assembled RNA sequence hopefully folds into the target structure. The GGI-Fold algorithm is implemented and tested on some biological data and the obtained results are compared with RNA-SSD algorithm.
The rest of this paper is organized as follows. In Section 2, some basic definitions are presented. In Section 3 and Section 4, a new method for the inverse RNA folding problem and some results are shown, respectively. Finally, the conclusion is presented in Section 5.
2. Basic Definition
An RNA molecule is composed of a long, usually single-stranded chain of nucleotide units: Adenine (A), Cytosine (C), Guanine (G) and Uracil (U). Thus, an RNA sequence of length ℓ in 5′-3′ direction can be represented as R = r1r2...rℓ, where |R| = ℓ and ri ∈ {A, C, G, U} (1 ≤ i ≤ ℓ).
The RNA secondary structure is formed by the creation of hydrogen bonds between Watson-Crick complementary bases (A−U and C−G) and sometimes between wobble base (G−U). In an RNA secondary structure, each base interacts with at most one other base, and form structures like stems and loops. Therefore, for an RNA secondary structure representation, we write (i, j) if the nucleotide with index i is paired with the nucleotide with index j (i < j). For an RNA sequence of length ℓ, its structure is represented by a set T of base pairs (i, j) where 1 ≤ i < j ≤ ℓ. Then for all (i1 , j1), (i2, j2) ∈ T, we have i1 = i2 if and only if j1 = j2 (each base can take part in at most one base pairing). The set T is called pseudoknot-free structure if for all (i1, j1), (i2, j2) ∈ T, they are either nested (i1 < i2 < j2 < j1) or disjoint (i1 < j1 < i2 < j2), as shown in Figure 1(Fig. 1).
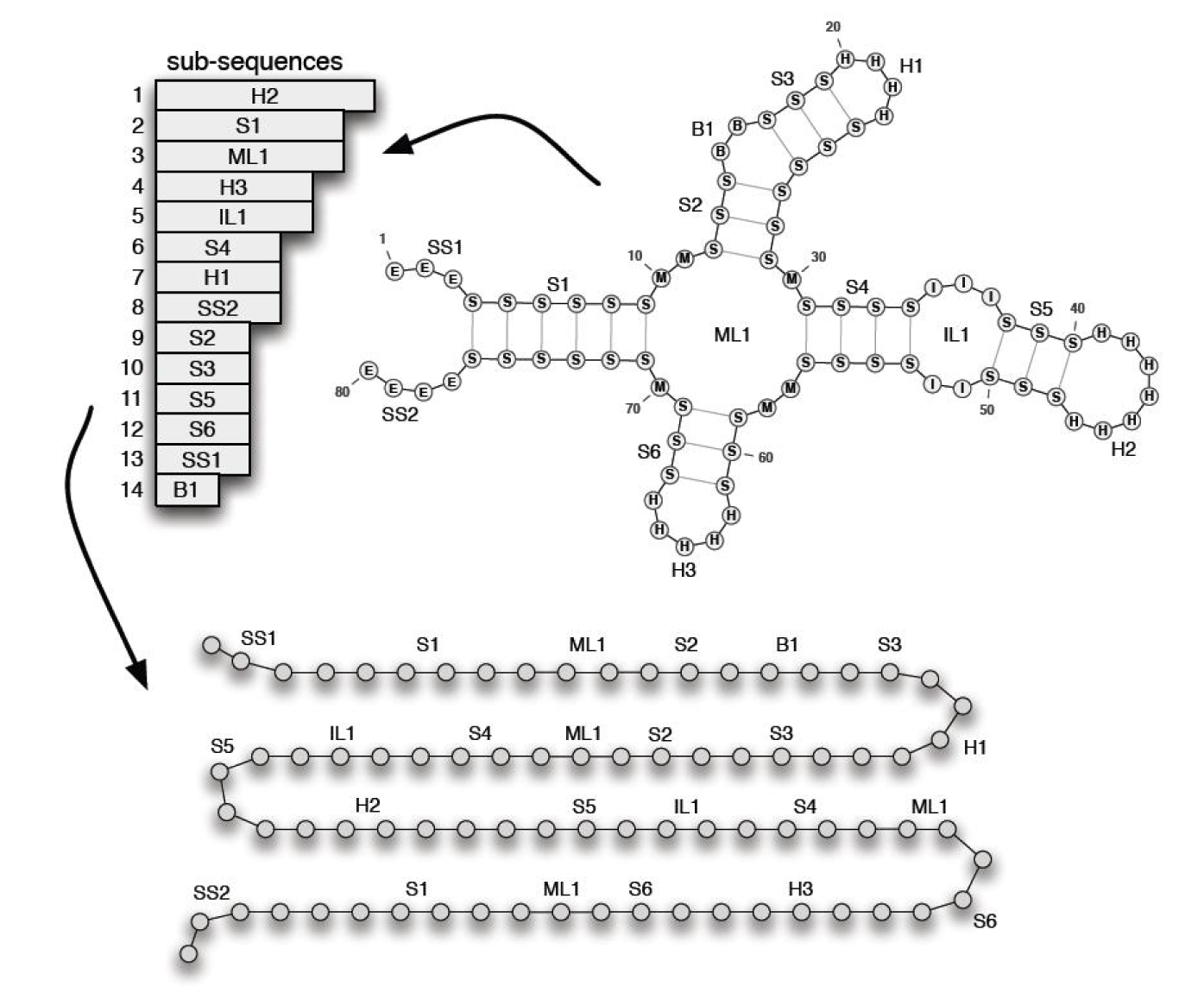
A pseudoknot-free secondary structure can be described as a string of balanced parentheses. In this representation, each two paired bases ri and rj, where (i, j) ∈ T, is represented by '(' and ')', respectively. Also, each unpaired base is represented by '.'. As mentioned, each RNA secondary structure is composed of stems and loops. A consecutive of base pairs is defined as a stem, and each consecutive of unpaired base is defined as a kind of loop. There are five different kinds of loops as follows: hairpin loop, bulge loop, internal loop, multiloop, and external loop. Each stem is represented by S and hairpin, bulge, internal, multi, and external loops are represented by H, B, I , M, and E, respectively. So, the given RNA secondary structure can be represented by its components list C = (c1, c2, ..., cn).For each i (1 ≤ i ≤ n) in this description, ci = (S, s1, e1, s2, e2) represents a stem, started from position s1 and ended in position e1 and the paired positions started from s2 and ended in e2. Also, ci = (L, s, e), where L ∈ {H, B, I , M, E}, represents a kind of loop, started from position s and ended in position e. For example, RNA secondary structure in Figure 1(Fig. 1) is decomposed into its components as follows:
C = ((E, 1, 4), (S, 4, 9, 76, 71), (M, 10, 11), (S, 12, 14, 29, 27), (B, 15, 16), (S, 17, 19, 26, 24), (H, 20, 23), (M, 30, 30), (S, 31, 34, 56, 53), (I , 35, 37), (S, 38, 40, 50, 48), (H, 41, 47), (I , 51, 52), (M, 57, 58), (S, 59, 61, 69, 67), (H, 62, 66), (M, 70, 70), (E, 77, 80)).
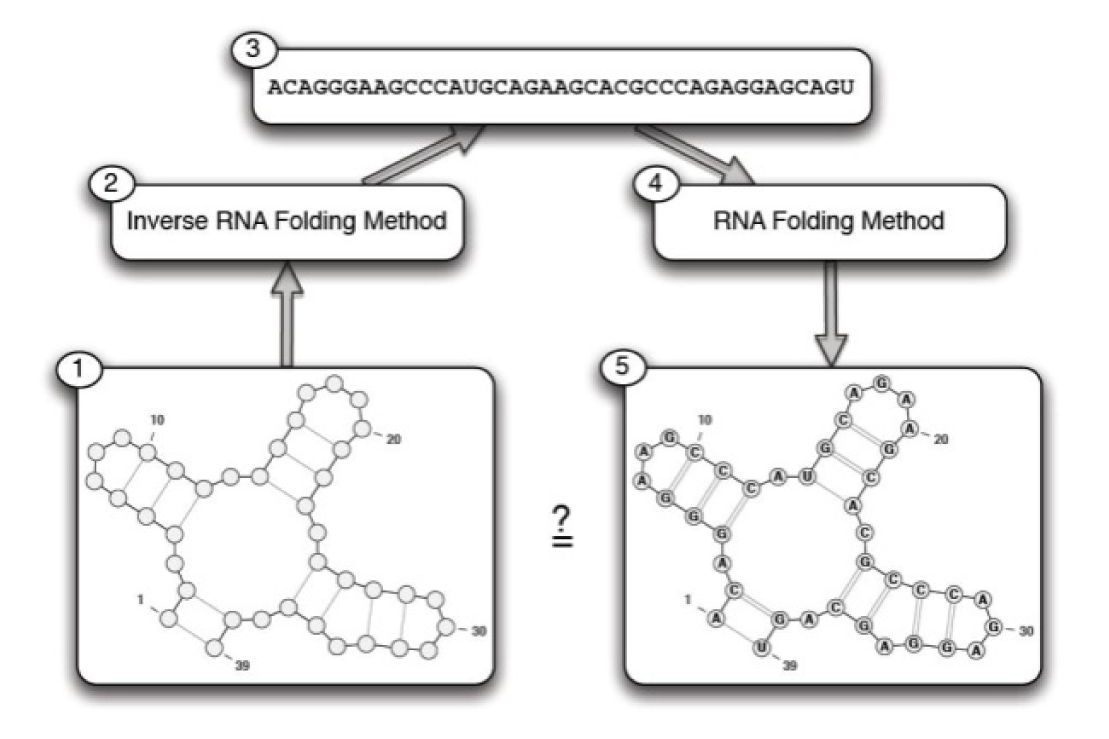
Based on the above discussion, the inverse RNA folding problem can be described as follows: an RNA secondary structure is given as an input (target structure) and the goal is to find an RNA sequence R = r1r2...rℓ, such that its secondary structure is the same (or very similar) to the given target structure.
3. Materials and Methods
In this section, we first explain how the real RNA dataset is reconstructed and then we present the details of our proposed methods.
3.1 Real RNA dataset
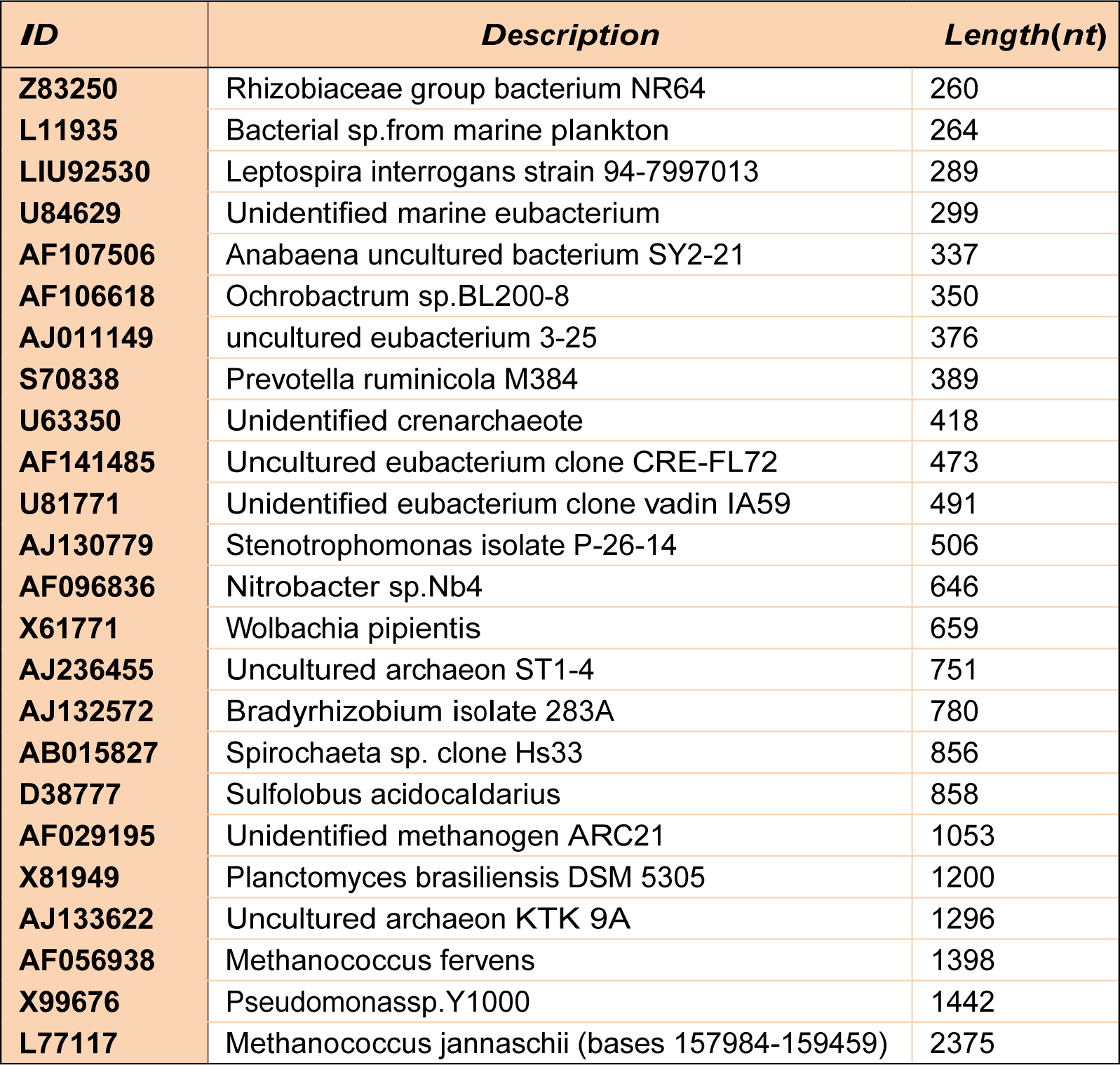
In order to compare the results of our proposed algorithm with the results of the other existing algorithms, we employ the same dataset of RNA sequences as presented in Andronescu et al. (2004[3]). This dataset contains 24 sequences of ribosomal RNA sequences (rRNAs) obtained from the RNA family database (Rfam). The Rfam (Griffiths-Jones et al., 2003[11]) is a collection of RNA families, primarily RNAs with a conserved RNA secondary structure. The names, descriptions, and lengths of these sequences are presented in Table 1(Tab. 1).
To determine the structures corresponding to the RNA sequences, we employ the RNAfold program (available as a part of Vienna RNA package). This program is implemented based on the Zuker's algorithm (Zuker, 1994[26]). To measure the quality of the generated results, the RNAdistance (from Vienna RNA package) is used to compute the structural distance between the target and generated structures.
3.2 A new method for inverse RNA folding problem
As mentioned, the goal of the inverse RNA folding problem is to design a sequence for the given target structure. In Figure 2(Fig. 2), the schematic representation of the inverse RNA folding problem is shown. In this section, we present a new algorithm based on multi-objective genetic algorithm and Gibbs sampling method for solving the inverse RNA folding problem. As it is mentioned, T is the given RNA secondary structure and C = (c1, c2, ..., cn) denotes the list of components appeared in T.
Let Z = (z1, z2, ..., zn) denotes the list of sub-sequences, where zi is a sub-sequence corresponding to the component ci. Let also Zj denotes the prefix of Z of length j, i.e. Zj = (z1, z2, ..., zj) (Z0 is an empty list). The main steps of our algorithm (GGI-Fold) are illustrated as follows:
1. The list C is decreasingly ordered by the length of its components.
2. For each k, 1 ≤ k ≤ n, call genetic algorithm MOGA (see section 3.2.1) with parameters ck and Zk−1. MOGA makes a sub-sequence zk according to the component ck and the generated sub-sequences in Zk−1.
3. The list Z is updated by Gibbs sampling method (see section 3.2.2).
4. All the generated sub-sequences in Z are assembled to make a sequence corresponding to the target structure T.
Since the longer sub-sequences are more important than the shorter ones, as well as they need more efforts to calculate their fitness values, so we first consider them. In the first step of the algorithm, the list C is decreasingly ordered based on the length of the components. In the second step of the algorithm, MOGA is performed on all components (from the longest to the shortest) to produce sub-sequences for each component. MOGA algorithm generates a sub-sequence for the current component based on the features of this component and all the previously generated sub-sequences for the longer components. However, we are not sure this ordering of the components to generate the sub-sequences is suitable enough. So, in the third step of the algorithm, all sub-sequences are updated by Gibbs sampling method, i.e. first a sub-sequence like zk is randomly removed from the list Z and then the algorithm MOGA is performed (with parameters Z and ck) to find a sub-sequence for ck. This method raises the dependency not only between small and large components, but also among all of them. Finally, when the algorithm cannot produce better sub-sequence, these sub-sequences are assembled to make an RNA sequence for the given structure T.
The details of the genetic algorithm MOGA (Step 2), Gibbs sampling method (Step 3), and the process of assembling the generated sub-sequences (Step 4) are discussed in the following subsections.
3.2.1 Generating the RNA sub-sequences by genetic algorithm
Genetic algorithm is a heuristic search method that mimics the process of natural evolution. This heuristic is used routinely to generate useful solutions to optimization and search problems. Genetic algorithms belong to the larger class of evolutionary algorithms, which generate solutions to optimization problems using techniques inspired by natural evolution, such as inheritance, mutation, selection, and crossover (Goldberg, 1989[10]).
In this section, our multi-objective genetic algorithm, MOGA, is introduced to design a sub-sequence for each component in the target structure. This algorithm prevents miss-hybridization as well as keeping the uniform chemical characteristics in the generated sub-sequences. Suppose that the component ck and the list Zk−1 are given to MOGA as inputs. In the population, each individual is an RNA sequence of length ℓk, where ℓk is the length of the component ck. Algorithm MOGA takes the component ck and the list Zk−1and generates the best sub-sequence (based on the fitness function) for the kth component with respect to the sub-sequences currently available in Zk−1, and the new generated sub-sequence is added to Zk−1 to produce the list Zk. The stopping condition is considered as a maximum number of regenerating the populations. We use the conventional genetic operations such as roulette wheel selection, one-cut-point crossover, and single-point mutation (Goldberg, 1989[10]).
Our genetic algorithm employs a multi-objective fitness function to evaluate the available solutions in the current population. The fitness function is the summation of five different measures. Four of these measures are introduced by Shin et al. (2005[21]) as follows:
5. ƒAU_content is a partial fitness function for counting the amount of A or U nucleotides in the sequence, which can be used to control the percentage of A/U or C/G in the designed sequences.
6. ƒSimilarity is a partial fitness function for preventing undesired hybridization by keeping the sequences as unique as possible in order to improve the accuracy of the generated sequences.
7. ƒContinuity is a partial fitness function for preventing occurrence of same bases continuously in a sequence in order to achieve the biologically relevance sequences.
8. ƒHybridization is a partial fitness function for preventing the potential hybridization in a loop. This can be done in a similar manner as ƒSimilarity, where a sub-sequence is checked against the reverse complement of the other sub-sequences.
The last part of the multi-objective fitness function is the minimum free energy (ƒMFE), which is the most important one in our genetic algorithm (Hofacker et al., 1994[14]). To consider these five different functions as a fitness function, we first scale them into the range of [0,1] and then totally add them up. Since each part of the multi-objective fitness function has its own importance, therefore a weight is assigned to each of them. The values of these weights are obtained experimentally. Therefore, the fitness function is calculated as follows:
Fitness= w1 × ƒAU_content+ w2 × ƒSimilarity + w3 × ƒContinuity +w4 × ƒHybridization + w5 ×fM F E,
where wis are the weights of each part in the fitness function. Note that the best fitness value is zero; therefore the genetic algorithm tries to minimize the fitness function.
3.2.2 Gibbs sampling method
In addition to the processing of components in decreasing order of their length, the Gibbs sampling method let us to process a random ordering for making sub-sequences. At first, the sub-sequences in the list Z are assembled to make a sequence R. In the second step, one of the generated sub-sequences, say zk , is randomly eliminated from the list Z to obtain a new list Z′. Then, MOGA is performed with inputs ck and Z′ to generate a new sub-sequence z′k corresponding to the component ck and add it to Z′. Then the new list Z′ is assembled to produce a new sequence R′. Later, the minimum free energies of the sequences R and R′ over the target structure are computed. If the minimum free energy of R′ is less than R, then, the list Z is replaced by the new list Z′. This process is repeated for 2 × n times, where n is the number of components. In this way, the quality of the generated sub-sequences is improved since each sub-sequence has a chance to be improved with respect to the other sub-sequences.
3.2.3 Assembling the sub-sequences
As mentioned, the sub-sequences corresponding to the components are generated by our genetic algorithm. Then, the quality of them is improved by Gibbs sampling method. To obtain the final result, these sub-sequences are simply assembled in the corresponding position of each component. This process is illustrated in Figure 3(Fig. 3).
4. Results
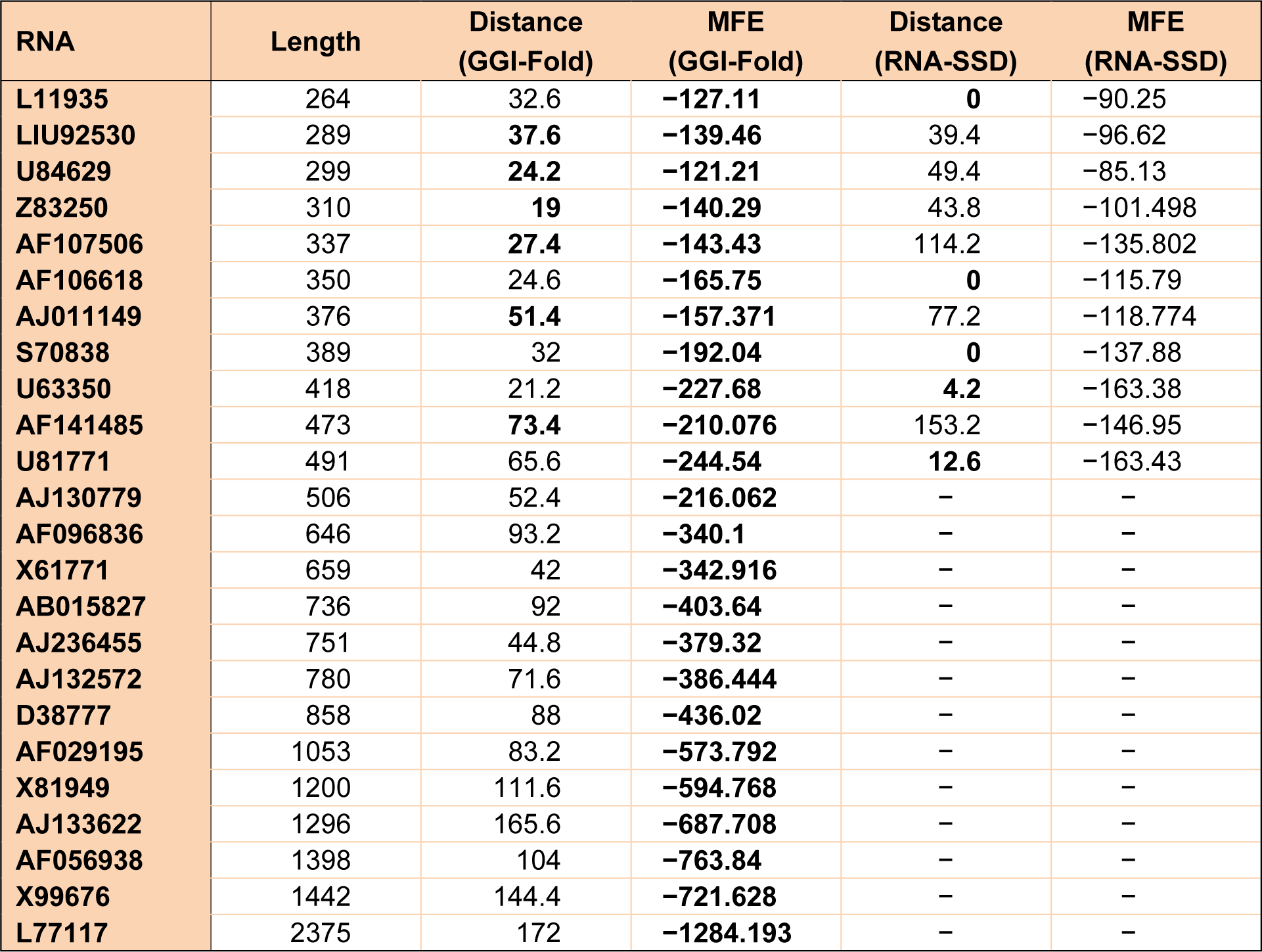
The GGI-Fold algorithm is implemented in C #.Net framework 3.5. We perform GGI-Fold on real RNA sequences taken from the RNA family database. The results of GGI-Fold algorithm over these sequences are compared to the results of RNA-SSD (Andronescu et al., 2004[3]) as indicated in Table 2(Tab. 2). As it is mentioned, the RNAdistance (available as a part of Vienna RNA package) is used to compute the structural distance between the target structure and the generated results.
Table 2(Tab. 2) has six columns. The first one, indicates the names of the RNAs which are extracted from Andronescu et al. (2004[3]). The second one, shows the length of these RNAs. The third one, represents the average structural distance between the target structure and the structures corresponding to the generated sequences. The fourth one, specifies the average free energies of the structures corresponding to the generated sequences. The fifth and sixth columns are the same as third and fourth columns for RNA-SSD, respectively. These averages are taken from 10 different executions of both algorithms. Since the RNA-SSD web server does not accept sequences of length greater than 500 bases, so the corresponding rows for these sequences are left blank in Table 2(Tab. 2). The comparison of the structural distance shows that our multi-objective genetic algorithm produces six samples better than RNA-SSD. Also the comparison of the minimum free energy shows that the structures of the designed sequences by GGI-Fold are more stable than those generated by RNA-SSD. The improved results are indicated as bold case in Table 2(Tab. 2) for both methods
5. Conclusions
The inverse RNA folding problem is considered in this paper as a multi-objective optimization problem. We used genetic algorithm and Gibbs sampling method to address this problem. We employed the genetic algorithm in an unusual way: instead of considering a population of chromosomes, each for a whole sequence, we break down the structure into some components and use the genetic algorithm for generating a good sub-sequence for each component. In this way, the generated sub-sequences are far from each other as much as possible. Also, instead of using the structural distance as a single measurement, we have employed five different measures to obtain the more reliable results. It should be mentioned that no folding algorithm has been employed to evaluate the accuracy of the generated sequences. As mentioned by Aguirre-Hernández et al. (2007[1]), interactions between RNA molecules are of substantial biological interest, and the RNA inverse algorithms can be extend to the design of duplexes of interacting RNAs (Alkan et al., 2006[2]; Montaseri et al., 2011[18]). The GGI-Fold algorithm can be extend easily for designing pairs of RNA strands that interact together.
Acknowledgements
This work is dedicated to Prof. Hayedeh Ahrabian, who is passed away on July (2011).
This research is supported by the Institute for Studies in Theoretical Physics and Mathematics (IPM) with grant number: 89680067.
References
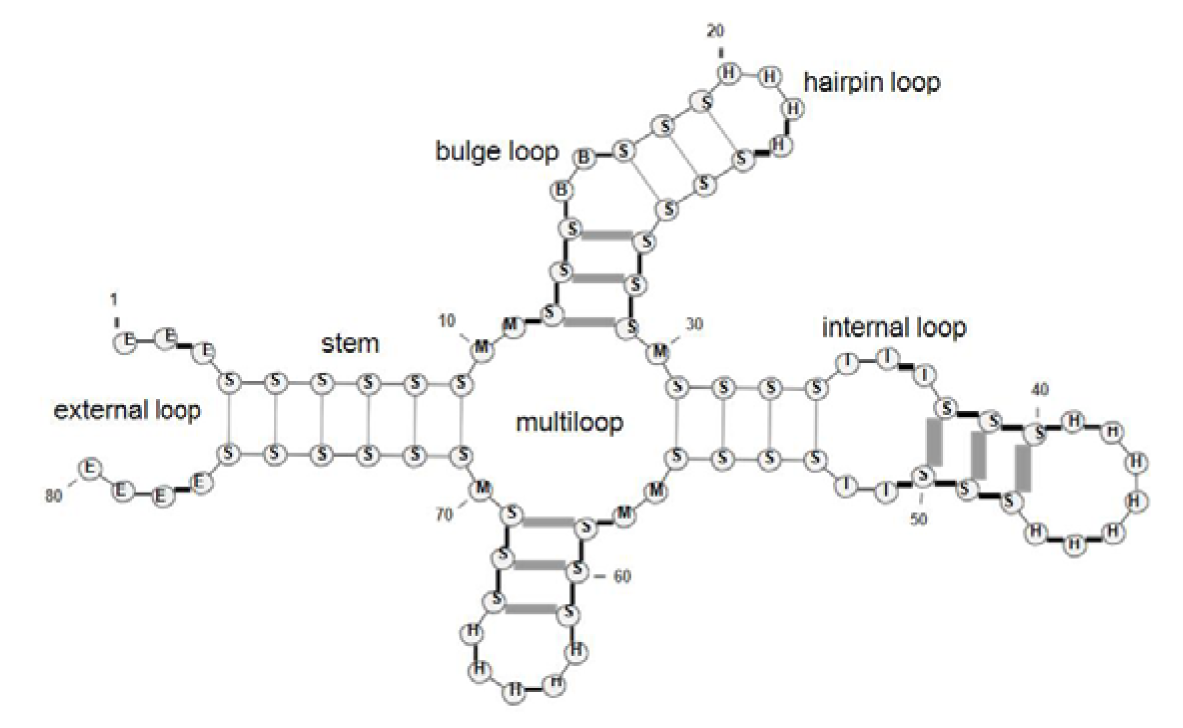
Figure 1: Schematic representation of stem and different kinds of loops in a RNA secondary structure
[*] Corresponding Author:
M Ganjtabesh, School of Mathematics, Statistics, and Computer Science, College of Science, University of Tehran, Tehran, Iran, eMail: mgtabesh@ut.ac.ir