Research article
Plant traits with different dimensions of shrubs represent different spatial patterns and plant-to-plant interactions in a temperate desert
Ye Tao1,2, Yuan Ming Zhang1[*],2
1Key Laboratory of Biogeography and Bioresource in Arid Land, Xinjiang Institute of Ecology and Geography, Chinese Academy of Sciences, South Beijing Road 818, Urumqi, Xinjiang 830011, China2University of Chinese Academy of Sciences, Yuquan Road 19 (A), Beijing 100049, China
EXCLI J 2013;12:Doc658
Abstract
Projective cover (PC) and aboveground biomass (AGB) are the key traits with space attributes of individual plants. They are crucial to the understanding of the plant dynamics and plant patterns at population level. Spatial patterns based on individual plant positions (IND) have been extensively investigated in previous studies. However, very few have focused on PC and AGB. We tested the hypothesis that different plant traits represent different spatial patterns and plant-to-plant interactions. Two 40 m × 40 m plots of two typical desert shrub populations (Seriphidium terrae-albae and Artemisia songarica) were surveyed in the Gurbantunggut Desert of north-western China. Each plot was divided into a series of subplots (grids) at different scales (17 scales from 0.5 m to 20 m) using GIS (geographic information system). The spatial patterns of IND, PC and AGB were determined using aggregation and information dimension analyses together with changes in the scales. The IND and AGB of the two populations exhibited clumped tendencies at all scales (except at the 0.5 m scale for S. terrae-albae), whereas PC showed uniform distribution patterns at the moderate and small scales, (0.5 m to 8.0 m for S. terrae-albae and 0.5 m to 4.0 m for A. songarica), indicating that crown-to-crown competition for sunlight was strong at these scales. Although IND had a slightly higher coefficient of variation at the small scales, its information dimension was smaller than those of PC and AGB, indicating that PC and AGB had higher spatial complexities. In conclusion, the three parameters represented different spatial patterns across multiple scales; PC and AGB showed strong spatial complexities and PC was also an accurate indicator of plant-to-plant competition.
Keywords: spatial complexity, projective cover, biomass, information dimension, aggregation analysis, plant location
Introduction
The spatial patterns and complexities of plant populations are crucial to the understanding of the structure and dynamics of populations and communities (Condit et al., 2000[6]; Li, 2000[14]). Spatial patterning also reveals interactions between plants, such as (e.g. competition, exclusion and self-thinning) and their relationship with the environment (Getzin et al., 2008[11]; Vacchiano et al., 2011[24]). There is a growing interest in scale-dependent analysis of spatial patterns at the population level (Stoyan and Penttinen, 2000[22]; Wu, 2000[27]; Getzin et al., 2008[11]). Until recently, the individual plant positions (IND) have frequently been used to investigate the spatial dynamics of plant populations (Diggle, 1983[7]; Zhang, 2004[29]; Getzin et al., 2008[11]). However, IND represents only points, in other words, is 0-dimensional, and simply indicates the number of plants and their locations. In contrast, two other parameters (plant traits), namely projective cover (PC) and aboveground biomass (AGB), not only show the plant locations, the number of plants and the quantity of biomass, but also the space attributes.
PC is characterized as a surface or a plane (2-dimensional), whereas AGB represents the individual plant volume (3-dimensional). Plant PC represents the overall effective photosynthetic area (Li, 2000[14]; Yang et al., 2008[28]). Studies have also shown that the spatial patterns based on the centers of projective crown areas (PC) can advance the understanding and evaluation of competition processes and patterns at the population level (Getzin and Wiegand, 2007[10]; Getzin et al., 2008[11]; Vacchiano et al., 2011[24]). On the other hand, AGB reflects the spatial accumulation, allocation and distribution of photosynthetic yield at the plant component and population levels. Therefore, the heterogeneity of AGB and PC at the population level can also represent the heterogeneity of sunlight, nutrient and water resources (Getzin and Wiegand, 2007[10]). Assuming that individuals of a population can exhibit a regular and uniform distribution, for example in plantations, elsewhere PC and AGB may not show a uniform distribution because of differences in body sizes (Ma and Zu, 2000[17]). Conversely, in a given population, the pattern of PC may be more uniform than that indicated by IND as a result of plant-to-plant competition. For example, in order to maximize light harvesting, the pattern of crown centroids (the center of the PC rather than the PC itself) may be more consistent than tree trunks in a mature forest stand (Vacchiano et al., 2011[24]). Therefore, using three different parameters to represent different population attributes, what are the spatial distribution patterns IND, PC and AGB at any given scale? What spatial complexity do these parameters reveal at varying scales and do they display the same patterns?
Some studies have suggested that point pattern analysis is the best method to characterize population spatial patterns (Diggle, 1983[7]; Zhang, 2004[29]). However, this is based only on the IND, which considers one position for one individual (Diggle, 1983[7]; Zhang, 2004[29]). The canopy areas and AGBs of different plants vary because of the differences in their size. The distances between INDs are obvious; however it is not possible to define the distances between PCs or AGBs as they belong to a plane or to a space. The point pattern analysis is therefore fundamentally unsuitable for PC and AGB, although the analysis can express the changes in the distance scales between individuals. A uniform standard of comparison must be followed if the three parameters, PC, AGB and IND, are to be considered. The grid-based method, generally used for individual numbers, may be feasible and a suitable technique that can be used to analyze and compare the parameters. In this method, IND, PC, and AGB, can be partitioned into different grids (subplots), with each grid containing a certain number (≥ 0) of parameter values. The two pattern analyses, namely, aggregation (Lloyd, 1967[16]; Moore and Bhadresa, 1978[20]; Shorrocks and Rosewell, 1988[21]) and information dimension (Li 2000[15]; Chen et al., 2005[5]), can then be used. The former determines the patterns (clumped, uniform, and random distributions) at certain scales and evaluates the significance at the 0.05 or 0.01 levels, whereas the latter represents the spatial complexity across multiple scales (Mandelbrot, 1982[18]; Falconer, 1990[8]). In addition, the AGB distribution of one shoot is complex, particularly in trees, and the components have uneven biomasses. For example, the stem occupies a small space but contains most of the biomass, while, the plant overstorey occupies most of the space, but has a relatively small biomass. In contrast to studies of temperate regions, desert shrubs have relatively consistent shapes with dense and uniform branches. Thus, the plant volume is approximated as a cylinder (Moore and Bhadresa, 1978[20]) and their biomass might be considered to be evenly distributed in the canopy.
To answer the above questions, we chose two small desert shrubs [Seriphidium terrae-albae (Krasch.) Poljak. and Artemisia songarica Schrenk, both Asteraceae] as target plants and used aggregation and information dimension analyses (based on grids) to determine and compare the spatial patterns (clumped, random, or uniform distributions) of the three parameters (IND, PC, and AGB) as well as changes in the structural complexity as a function of scale. We hypothesized that the three parameters with different dimensions represent different spatial patterns and plant-to-plant interactions at certain scales and that the patterns change with the scale.
Materials and Methods
Study area and plant materials
The study site (44°95 N, 87°76 E) is located at the center of the Gurbantunggut Desert, Xinjiang, in north-western China. The Gurbantunggut is the second largest (4.88 × 104 km2) desert in China, and is also a typical temperate desert of the world. The annual precipitation is approximately 70 to 150 mm, whereas the mean annual pan evaporation exceeds 2,000 mm. The average annual temperature is 5 °C to 7 °C. Wind speeds reach their maximum from April through to July, with an annual average of 11.17 m/s (Wang et al., 2003[25]). The desert is covered by massive, dense, semi-fixed sand dunes, with much of the surface covered by biological soil crusts (BSCs) composed of cyanobacteria, lichens and mosses (Zhang et al., 2010[31]). The desert has 208 vascular plants and 18 different plant communities. The natural vegetation is dominated by two small trees: Haloxylon persicum Bunge ex Boiss. and Buhse and Haloxylon ammodendron (C. Mey) Bunge. A number of shrubs, such as Ephedra distachya L., S. terrae-albae, A. songarica and Calligonum leucocladum (Schrenk) Bunge, are widely distributed but scattered among the sand dunes. The desert also has abundant and varied ephemeral and ephemeroid species (Zhang and Chen, 2002[30]).
The two target shrubs (S. terrae-albae and A. songarica) occupy different habitats. Populations of S. terrae-albae are primarily distributed from the midpoint to the lowest point of sand dunes, where the ground is commonly covered by BSCs. In contrast, A. songarica populations generally thrive on bare sand and in disturbed areas on the crests of sand dunes where BSCs are absent or poorly developed. Both target shrubs have dense branches and relatively uniform shapes, making them particularly suitable for this study.
Vegetation sampling and aboveground biomass estimation
The field sampling was carried out from the 12th to the 14th July, 2010. Two study sites with gently sloping terrain were selected. The size of each population sampling plot was 40 m × 40 m (Figures 1a, 1b(Fig. 1)). Each plot was divided into 400 contiguous 2 m × 2 m quadrats, the basic units of this vegetation survey. The relative location of each individual, the crown length (CL, at the widest point, in m), crown width (CW, at the shortest point, in m), and height (H in m) were recorded. Finally, two 40 m × 40 m coordinate systems showing the plant positions were generated on the computer.
The AGB of each shrub was estimated using a general nonlinear allometric equation, Y = aCHb, where Y is AGB, a is the normalization constant and b is the allometric scaling exponent. CH is the canopy volume (in m3), which was estimated by:
CL/2 × CW/2 × π × H.
The equations of the two shrubs were described as
AGB(S. terrae-albae) = 631.34 × (CH)0.814 (n = 30, R2 = 0.918) and
AGB(A. songarica) = 525.98 × (CH)0.931 (n = 30, R2 = 0.923).
Scale partitioning in spatial pattern analyses
IND, PC, and AGB have different dimensions. Hence, these three parameters were placed in the same platform for comparison. Each 40 m × 40 m plot (Figures 1a, 1b(Fig. 1)) was divided into a series of subplots (grids) at different scales using the ArcGIS v9.3 software (Table 1(Tab. 1)). The numbers/amounts (i.e. the number of individuals as well as the PC and AGB in each subplot) of the three parameters in the subplots at the same scales (Figures 1c-e(Fig. 1)) were used to compare the spatial patterns. A total of 17 distance scales (m) were established. The maximum and minimum side lengths of the subplots were 20.0 m (4 subplots) and 0.5 m (6400 subplots), respectively (Table 1(Tab. 1)). All 17 scales were used in the information dimension analysis. Of these, seven scales, namely, 0.50, 1.00, 2.00, 4.00, 5.00, 8.00, and 10.0 m, were used in the aggregation analysis.
The partitioning of IND at each scale, (determining the number of individuals partitioned in the different subplots, Figure 1c(Fig. 1)), was more straightforward than partitioning of PC and AGB. For PC partitioning, the canopy lengths and widths showed negligible differences. The canopy area of each shrub was nearly circular and was therefore calculated as a circle [Area = (L/4 + W/4)2 × π]. When the shrubs were sparse and non-overlapping, the actual PC was equal to the sum of canopy areas of the shrubs (Figure 1d(Fig. 1)). Meanwhile, if the shrubs overlapped each other, the actual total PC was smaller than the total canopy areas of all shrubs. This process was performed by the union function of the ArcGIS v9.3 software. The PC of one individual was divided into several parts at certain scales and was then partitioned in different subplots (Figure 1d(Fig. 1)).
The partition method for AGB was also different from IND and PC. It was important that the AGB in the overlapping region not be ignored (Figure 1e(Fig. 1)). The volume (3-dimensinal) was then translated into a plane (2-dimensinal). The target shrubs showed significant branching, with branches that were soft and often bent outwards. Hence, the volume (shape) was approximated as a circular cylinder, whereas the vertical section of the shrub was represented a rectangle (Moore and Bhadresa, 1978[20]). The AGB of one individual was assumed to be equally distributed in the individual canopy area (i.e. cylindrical) for convenience of calculation. The AGBs partitioned in different subplots at a given scale were calculated using the proportion of each part to the individual canopy area. The AGB in the overlapped region was calculated using the intersection function of the ArcGIS v9.3 software.
Aggregation analysis
Three distribution patterns (clumped, random and uniform) have been observed in natural plant populations (Li, 2000[14]). We performed the analyses of the IND, PC and AGB clumping degrees using the variance-to-mean ratio (VMR), the Morisita index (Is) and Lloyd's index (L) (Lloyd, 1967[16]; Moore and Bhadresa, 1978[20]; Diggle, 1983[7]; Zhang, 2004[29]) at 0.5, 1.0, 2.0, 4.0, 5.0, 8.0, and 10.0 m scales.
VMR = 1 indicates a random distribution, VMR < 1 means a uniform distribution, and VMR > 1 represents a clumped distribution. The significance testing of clumping (when VMR > 1) was performed using the t-test [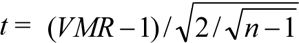 , where n is the number of subplots at each scale]. A t > t0.05(n-1) indicates considerable clumping (P < 0.05), whereas t > t0.01(n-1) indicates highly significant clumping (P < 0.01). The t0.05(n-1) or t0.01(n-1) value was obtained from the t distribution table. Is was calculated as n(ΣX2-ΣX)/(ΣX)2-ΣX), where X is the parameter value in each subplot. Is = 1 indicates random distribution, Is < 1 means a uniform distribution, and Is > 1 indicates a clumped distribution. The significance of the clumped distribution (when Is > 1) was determined using the F-test, where F = (Is ΣX-1 + n -ΣX)/ (n-1). F > F0.05(n-1, ∞) indicates considerable clumping (P < 0.05) and F > F0.01(n-1, ∞) represents highly significant clumping (P < 0.01). The F0.05(n-1, ∞) or F0.01(n-1, ∞) value was obtained from the F distribution table.
, where n is the number of subplots at each scale]. A t > t0.05(n-1) indicates considerable clumping (P < 0.05), whereas t > t0.01(n-1) indicates highly significant clumping (P < 0.01). The t0.05(n-1) or t0.01(n-1) value was obtained from the t distribution table. Is was calculated as n(ΣX2-ΣX)/(ΣX)2-ΣX), where X is the parameter value in each subplot. Is = 1 indicates random distribution, Is < 1 means a uniform distribution, and Is > 1 indicates a clumped distribution. The significance of the clumped distribution (when Is > 1) was determined using the F-test, where F = (Is ΣX-1 + n -ΣX)/ (n-1). F > F0.05(n-1, ∞) indicates considerable clumping (P < 0.05) and F > F0.01(n-1, ∞) represents highly significant clumping (P < 0.01). The F0.05(n-1, ∞) or F0.01(n-1, ∞) value was obtained from the F distribution table.
Lloyd's index L = m + VMR - 1, where m is the mean, was also obtained. L/m = 1 indicates a random distribution, L/m < 1 a uniform distribution, and L/m > 1 represents a clumped distribution. L/m was nearly equal to Is (Miao, 1991[19]), hence, we did not show the results of our calculation for Lloyd's index.
Information dimension analysis
The Shannon information entropy Hε(x) was calculated as follows (Li, 2000[15]; Chen et al., 2005[5]):
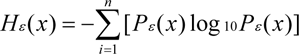
where Pε(x) is the percentage or ratio of the number of individuals, PC or AGB (x) in the ith subplot to the total amount and n is the number of subplots in a given scale. A low Hε(x) value represents a simple parameter structure, whereas high entropy indicates a more complicated structure. Entropy is related to the scale (ε).
The information dimension (DI) at each scale ε was used to measure the complexity or the change in Hε(x) at different scales, as well as the heterogeneity of a parameter. DI was estimated using the following (Li, 2000[15]; Chen et al., 2005[5]) equation:
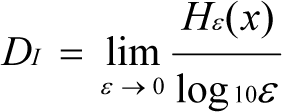
The calculation for DI was conducted using the model type I (ordinary least squares, OLS) regression protocol. A one-way ANOVA was used to evaluate the differences in the regression curve parameters. The standard error (SE) of DI was also obtained. The regression and one-way ANOVA were performed using the software “Standardized Major Axis Test and Routines, SMATR” (Warton and Weber 2002[26]; Falster et al., 2003[9]). In addition, the coefficient of variation (CV = standard deviation/mean) was used to quantify the variation in, or stability of, each target parameter at each scale.
Results
Descriptive statistics of two populations
A total of 1,182 individual samples of S. terrae-albae in a S. terrae-albae plot and 1,160 A. songarica specimens in an A. songarica plot were analyzed (Table 2(Tab. 2)). The average canopy diameters of S. terrae-albae and A. songarica were 38.01 and 58.69 cm, respectively. The total individual canopy areas were 145.45 and 347.38 m2 for the S. terrae-albae and A. songarica plots, respectively, and the average canopy areas per individual were 0.123 and 0.230 m2. The total projective covers were slightly less than those of canopy areas of S. terrae-albae (1.07 m2) and A. songarica (26.85 m2), and the proportions of the overlapped area to the total individual canopy area were 0.74 % for the former and 7.73 % for the latter. The total AGBs in the S. terrae-albae and A. songarica plots were 49.71 and 94.17 kg, respectively, whereas the AGBs per individual were 42.06 and 81.18 g. Lastly, the AGBs per unit canopy areas for the S. terrae-albae and A. songarica plots were 341.77 and 271.09 g, respectively.
Distribution and aggregation patterns of the three parameters
The IND of the S. terrae-albae population showed significantly clumped distributions at the 1.0 m to 10.0 m scales but exhibited a uniform distribution at the smallest scale (0.5 m). On the other hand, the IND of the A. songarica population showed clumped distributions at all seven scales (0.5 m to 10.0 m) (Table 3(Tab. 3)). The AGB values of the two populations exhibited remarkably significant (P < 0.01) clumped distributions at all scales. Meanwhile, the PC values of the S. terrae-albae population presented a uniform distribution at the 0.5 m to 8.0 m scales and a clumped distribution (not significant) at the 10.0 m scale, whereas those of A. songarica population showed uniform distributions at the 0.5 m to 4.0 m scales and clumped distributions at the 5.0 m to 10.0 m scales. Therefore, PC showed a uniform distribution at most of the study scales, whereas IND and AGB predominantly exhibited clumped distributions. The regular distribution patterns of PC indicated that the crown-to-crown competition for sunlight was strong at both moderate and small scales.
The aggregation strengths (VMR values) of the three parameters increased with increasing scales (Table 3(Tab. 3)). The VMR value of each parameter of the A. songarica population was clearly higher than that of the S. terrae-albae population at each scale. At the same scale, the spatial patterns of the different parameters were slightly different. Consequently, the patterns and aggregation strengths of each parameter were different at different scales.
Information dimension of the three parameters across multiple scales
The CVs of the three parameters decreased with the increase in scales (Figure 2(Fig. 2)). The three parameters of the S. terrae-albae population exhibited high variations (CV > 1) at the 0.5 m to 1.0 m scales, whereas those of the A. songarica population showed high variations at the 0.5 m to 1.33 m scales. At all scales, the CV of each parameter of the A. songarica population was higher than that of the S. terrae-albae population. In addition, the IND of the A. songarica population showed higher variation compared with those of PC and AGB.
For both populations, the IND had the smallest information dimension (DI) values. On the other hand, PC had the highest DI, despite the non-significance of the DI values of PC to the AGB values (Table 4(Tab. 4)). Therefore, IND exhibited a lower spatial complexity compared with that of PC and AGB. In addition, the determination coefficients (R2) of IND for both shrubs were less than those of PC and AGB, indicating that the Shannon information entropy Hε(x) of IND was more unstable.
Discussion
The three different plant parameters (IND, PC, AGB) represented somewhat different spatial patterns across multiple scales. IND, PC, and AGB exhibited different dimensions and spatial attributes, including spatial positions (individual number), leaf photosynthetic area, and allocation and accumulation of photosynthetic products (or organic C). The commonly used IND primarily showed clumped distributions at all scales; the same result was obtained for AGB. Meanwhile, PC exhibited uniform distributions at relatively moderate and small scales (0.5 m to 8.0 m for the S. terrae-albae population and 0.5 m to 4.0 m for the A. songarica population), indicating a uniform capacity to harvest solar radiation resulting from competition between plants. However, PC exhibited clumped distributions at relatively larger scales, indicating obvious scale-change characteristics. Organic C (biomass) is one of the bases of the earth's biomes and is known to exhibit uneven distributions at the macro scale (e.g., different continents and latitudinal zones) as well as in various ecosystems and soil types (Houghton et al., 2009[12]). Organic C has also shown non-uniform distribution at regional (e.g. Sonoran Desert, Búrquez et al., 2010[4]) and small scales (Baishya et al., 2009[2]; Zhu et al., 2011[32]). In this study, the AGBs of shrub populations also showed uneven distribution at the micro scale (0.5 m to 20.0 m). It is worth noting that PC exhibited a relatively uniform distribution when compared to IND and AGB at small and intermediate scales. This may constitute a crown architecture trade-off among individuals at population level (Koichi and Yumi, 2008[13]) as a result of crown-to-crown competition for sunlight at moderate and small scales (Getzin et al., 2008[11]).
Population spatial pattern is the result of long-term interaction and co-adaptation between a population and its environment (Zhang, 2004[29]). The relationships between population and the environment are determined by (1) the ecological and biological characteristics as well as the ecological process of inter/intraspecific competition and (2) the habitat or environment, including elements such as water, nutrients and sunlight. As a result of these relationships, the clumped distribution has become the most common form of plant population spatial patterning in terrestrial ecosystems based on the IND (Li, 2000[14]) and including AGB. Although the descriptive statistics (where plant size and percentage of small individuals in the A. songarica population exceed those in the S. terrae-albae population) and habitats of the two shrub populations were clearly different, the same plant parameter showed similar spatial patterns at the given scales (see aggregation patterns in Table 3(Tab. 3)) and exhibited similar change tendencies (see information dimension in Table 4(Tab. 4)) across multiple scales. These results imply generality, which is independent of the population type. The clumped strengths of all parameters of the two shrub populations were also different. In this study, the S. terrae-albae population was associated with higher levels of soil nutrients and greater species diversity (particularly herbaceous plants) than the A. songarica population (Tao and Zhang, 2011[23]). The former also had more abundant resources for survival and development when compared with the latter. Also, wind speed was higher on areas of bare sand, mostly at the crest of sand dunes, than it was on low lying areas covered by BSCs (Wang et al., 2003[25]), thus reducing the opportunity for seed germination and litter accumulation on the areas of bare sand. Unlike the S. terrae-albae population plot, which was covered by BSCs, seeds and accumulated litter from the A. songarica population growing on bare sand, were mostly clustered around the parent plants; there was little in the way of seeds and litter on patches of ground which lacked shrubs. These conditions contribute to the lack of uniformity in distribution of soil nutrients and of individual plants (Yang et al., 2008[28]). These factors may also be an important cause of the clumped distribution of the A. songarica population. Allelopathy and self-thinning generated by the parent plants may also contribute to the uneven distribution of seedlings.
The information dimensions of IND for both populations were low, indicating low structural complexities. The high information dimensions of PC and AGB may be related to their space related traits. The determination coefficients (R2) of IND for both shrubs were lower than those for PC and AGB, indicating that the Shannon information entropy Hε(x) of IND was more unstable. Moreover, the CVs of IND were more unstable than those of PC and AGB, with IND having the largest values at the small scales.
With the steady increase in large-scale spatial data acquisition based on remotely sensed images, there is a growing demand to understand and evaluate forest stand dynamics based on tree-crown patterns (Atkinson et al., 2007[1]; Getzin et al., 2008[11]) since PC (or crown cover) can demonstrate spatial patterns and plant-to-plant interactions much more efficiently than IND and AGB. This is in spite of the fact that AGB has a similar spatial complexity to PC. The uniform distribution of PC at moderate and small scales is the structural adaptation of crown architecture to a heterogeneous light environment since canopy structure is mainly designed to maximize photosynthesis (Berezovskava et al., 1997[3]; Getzin and Wiegand, 2007[10]; Vacchiano et al., 2011[24]). Moreover, small scale competition may be due to competition-induced mortality over short distances (Vacchiano et al., 2011[24]). By contrast, in this study, IND and AGB contributed a relatively low competition intensity among individual plants than did PC, as the former parameters presented clumped distribution patterns at nearly all scales.
In conclusion, the three parameters represented different spatial patterns across multiple scales; PC and AGB showed strong spatial complexities and PC was also an accurate indicator of plant-to-plant competition. Thus IND, PC and AGB have reflected different aspects of population or community functions and these may contribute to a better understanding of the structure and function of plant populations.
Acknowledgements
We are grateful to Xiao-Bing Zhou and Zhi-Bin Zhou from Xinjiang Institute of Ecology and Geography, Chinese Academy of Sciences (Xieg, Cas) for their help with the field survey. We thank Xiao-Bo Wu from Xieg, Cas for technical support (ArcGIS software). We also thank Dong Qiu from Xinjiang Agricultural University for data preparation. Special thanks are due to Prof. Alison Downing from Department of Biological Sciences, Macquarie University, Australia, for her constructive comments on this manuscript. The National Natural Science Foundation of China (Nos. U1203301, 41201056), the West Light Foundation of the Chinese Academy of Sciences (No. XBBS201103) and the National Natural Science Foundation of China (Nos. 41271281, 41001181) supported this study.
References
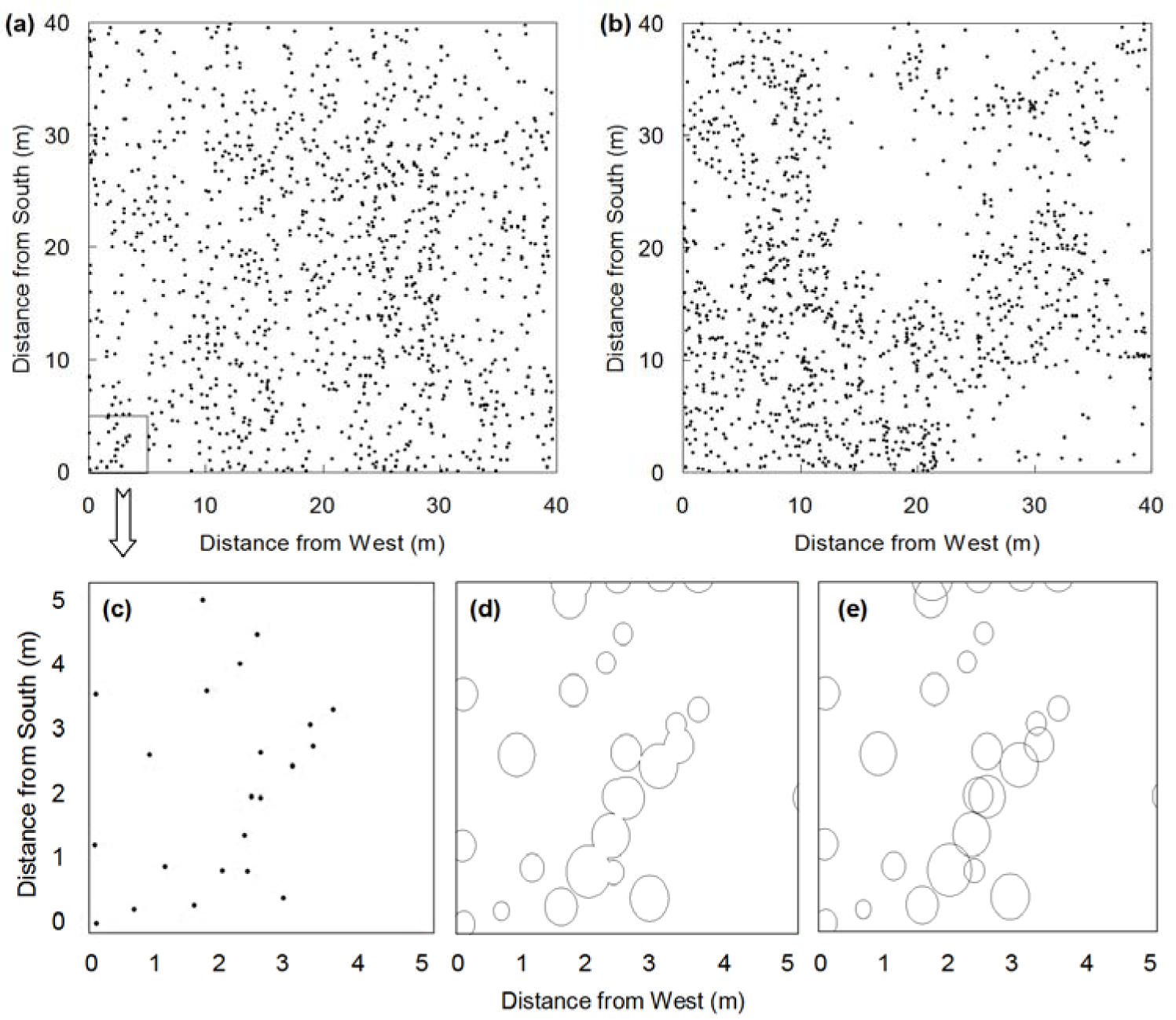
Figure 1: Individual distributions of (a) Seriphidium terrae-albae and (b) Artemisia songarica population plots (40 m × 40 m) at the center of the Gurbantunggut Desert, Northwest China. Diagrams of (c) individual points, (d) projective covers and (e) canopy areas (showing aboveground biomass) in one S. terrae-albae subplot (5 m × 5 m). The upper marginal area of the subplot [taken from (a)] contains (c) only one individual but includes (d) several projective covers and (e) biomass of other individuals located just outside the boundary of the subplot.
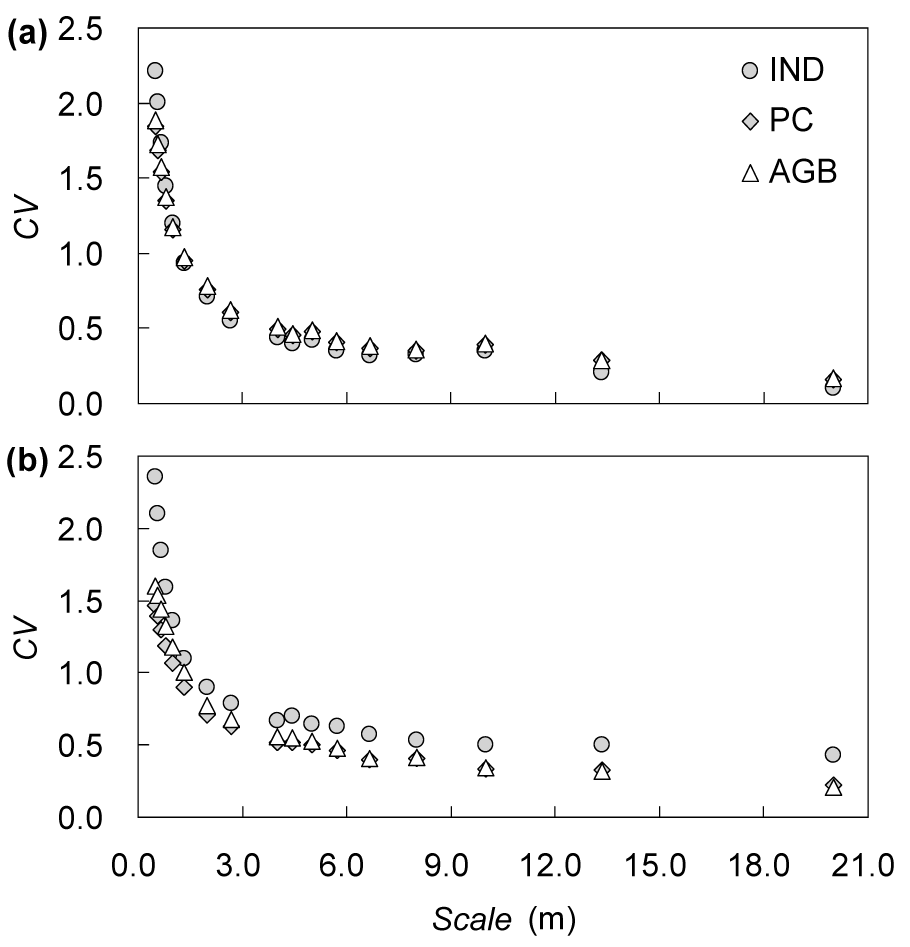
Figure 2: Coefficients of variation (CVs) of the three parameters (IND = individual number, PC = projective cover, AGB = aboveground biomass) in the (a) Seriphidium terrae-albae and (b) Artemisia songarica populations

Table 2: Characteristics of individual number (IND), canopy diameter (D), actual canopy area (CA), projective cover (PC) and aboveground biomass (AGB) of S. terrae-albae and A. songarica populations
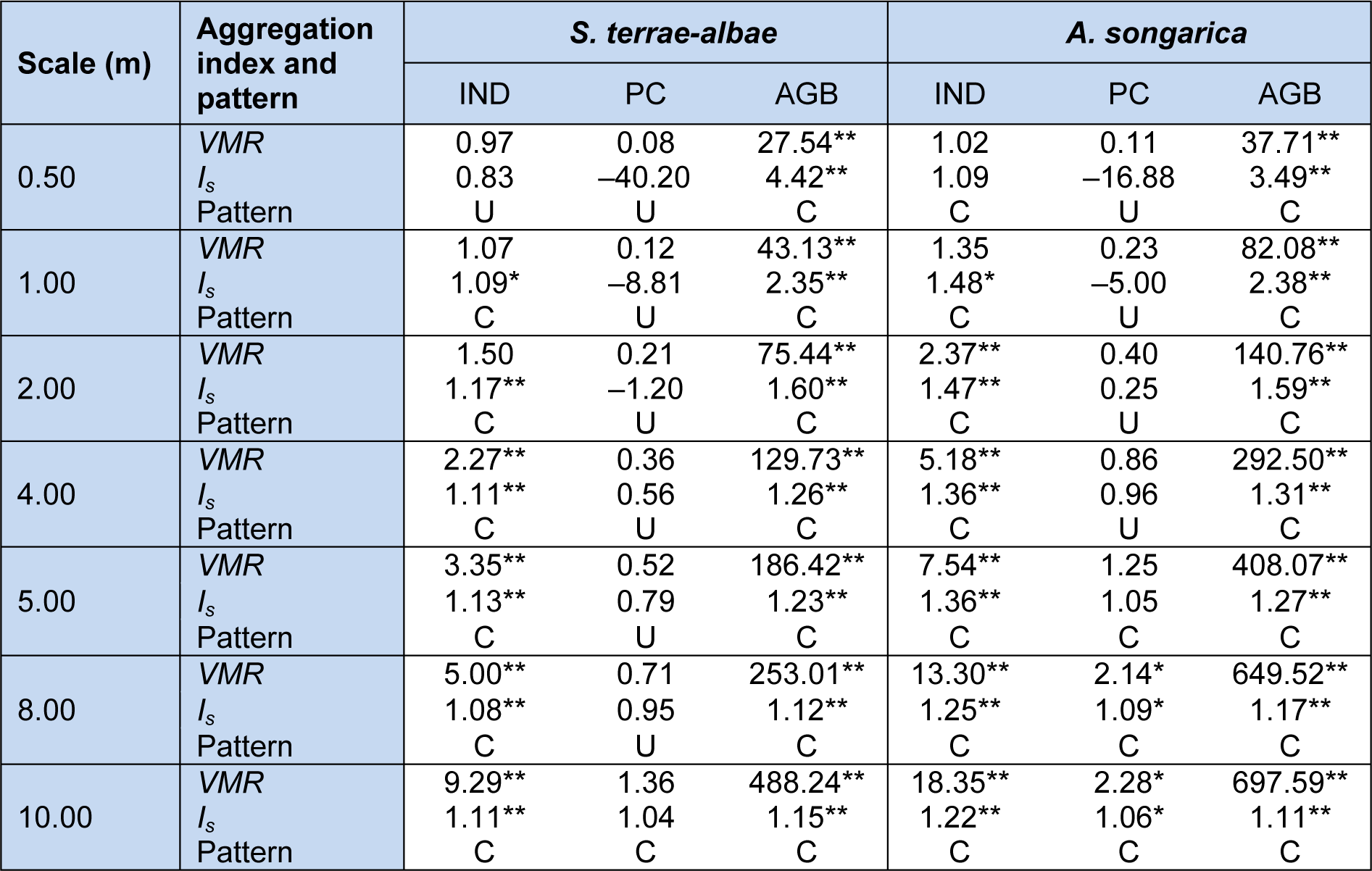
Table 3: Aggregation indices and the spatial patterns of three parameters (individual number, projective cover, aboveground biomass) in S. terrae-albae and A. songarica populations at seven scales. U refers to uniform distribution and C refers to clumped distribution. * indicates significant clumped (P < 0.05), ** indicates very significant clumped (P < 0.01). VMR = variance to mean ratio, Is = Morisita index value
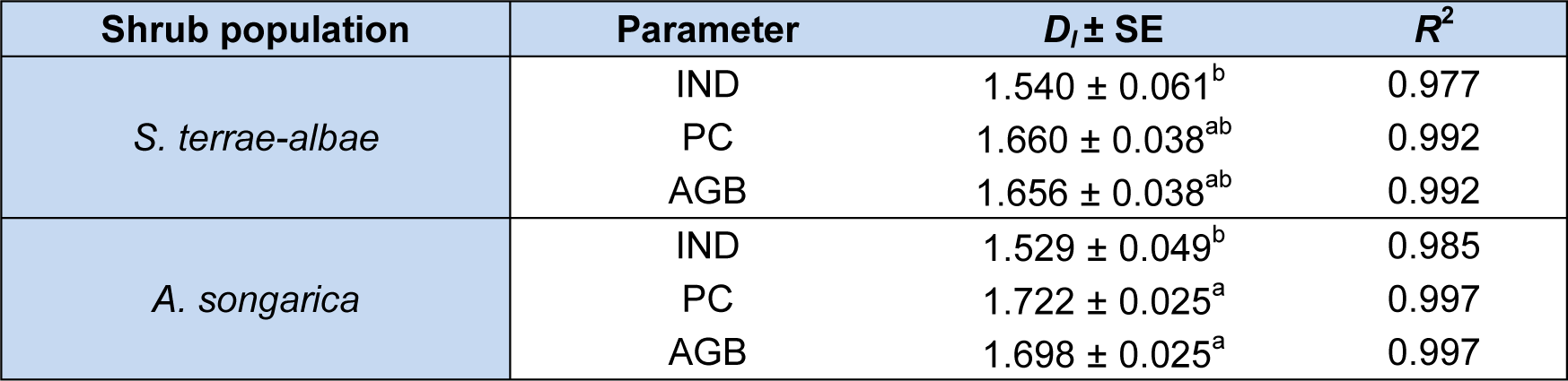
Table 4: Information dimension (DI) of three parameters (individual number, projective cover, aboveground biomass) in S. terrae-albae and A. songarica populations. All P values were less than 0.0001. Different letters indicate significant difference among six parameters of two shrubs (P < 0.05).
[*] Corresponding Author:
Yuan Ming Zhang, Key Laboratory of Biogeography and Bioresource in Arid Land, Xinjiang Institute of Ecology and Geography, Chinese Academy of Sciences, South Beijing Road 818, Urumqi, Xinjiang 830011, China; Tel: +86 991 7823158; Fax: +86 991 7823149, eMail: zhangym@ms.xjb.ac.cn